Теплопроводность

Теория теплопередачи, или теплообмена, представляет собой учение о процессах распространения теплоты в пространстве с неоднородным полем температур.

Существуют три основных вида теплообмена: теплопроводность, конвекция и тепловое излучение.

Теплопроводность — это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов).

Конвекция осуществляется путем перемещения в пространстве неравномерно нагретых объемов среды. При этом перенос теплоты неразрывно связан с переносом самой среды.

Тепловое излучение характеризуется переносом энергии от одного тела к другому электромагнитными волнами.

Часто все способы переноса теплоты осуществляются совместно. Например, конвекция всегда сопровождается теплопроводностью, так как при этом неизбежно соприкосновение частиц, имеющих различные температуры.

Совместный процесс переноса теплоты конвекцией и теплопроводностью называется конвективным теплообменом. Частным случаем конвективного теплообмена является теплоотдача — конвективный теплообмен между твердой стенкой и движущейся средой. Теплоотдача может сопровождаться тепловым излучением. В этом случае перенос теплоты осуществляется одновременно теплопроводностью, конвекцией и тепловым излучением.

Многие процессы переноса теплоты сопровождаются переносом вещества — массообменном, который проявляется в установлении равновесной концентрации вещества.

Совместное протекание процессов теплообмена и массообменна называется тепломассообменном.

Теплопроводность определяется тепловым движением микрочастиц тела. В чистом виде явление теплопроводности наблюдается в твердых телах, неподвижных газах и жидкостях при условии невозможности возникновения в них конвективных токов.

Передача теплоты теплопроводностью связана с наличием разности температур тела. Совокупность значений температур всех точек тела в данный момент времени называется температурным полем. В общем случае уравнение температурного поля имеет вид:

где t — температура тела; х, у, z — координаты точки; τ — время. Такое температурное поле называется нестационарным и отвечает неустановившемуся режиму теплопроводности. Если температура тела не изменяется с течением времени, то температурное поле называется стационарным. Тогда

Температура может быть функцией одной, двух и трех координат, соответственно температурное поле будет одно-, дву- и трехмерным. Наиболее простой вид имеет уравнение одномерного стационарного температурного поля:

Если соединить все точки тела с одинаковой температурой, то получим поверхность равных температур, называемую изотермической. Так как в определенной точке тела в данный момент времени может быть только одна температура, изотермические поверхности не пересекаются; все они либо замыкаются на себя, либо заканчиваются на границе тела. Пересечение изотермных поверхностей плоскостью дает на ней семейство изотерм. Интенсивность изменения температуры в каком-либо направлении характеризуется производной

, принимающей наибольшее значение в направлении нормали к изотермической поверхности

Вектор

называется температурным градиентом и является мерой интенсивности изменения температуры в направлении по нормали к изотермной поверхности. Направлен он в сторону возрастания температуры.

9.2.Закон Фурье

Согласно гипотезе Фурье, количество теплоты d²Q_τ, проходящее через элемент изотермической поверхности dF за промежуток времени dτ, пропорционально температурному градиенту

Здесь множитель λ называется коэффициентом теплопроводности. Знак минус указывает на то, что теплота передается в направлении уменьшения температуры. Количество теплоты, прошедшее в единицу времени через единицу изотермической поверхности, называется плотностью теплового потока:

(9.5)

Проекции вектора q на координатные оси соответственно:

;

Уравнения (9.4) и (9.5) являются математическим выражением основного закона теплопроводности — закона Фурье.

Количество теплоты, проходящее в единицу времени через изотермическую поверхность F, называется тепловым потоком:

(9.6)

Полное количество теплоты, прошедшее через эту поверхность за время τ, определится из уравнения

(9.7)

9.3.Коэффициент теплопроводности

Коэффициент теплопроводности является физическим параметром вещества, характеризующим его способность проводить теплоту. Коэффициент теплопроводности определяется из уравнения (9.4):

(9.8)

Численно коэффициент теплопроводности равен количеству теплоты, проходящему в единицу времени через единицу изотермической поверхности при условии gradt=1. Его размерность Вт/(м·К). Значения коэффициента теплопроводности для различных веществ определяются из справочных таблиц, построенных на основании экспериментальных данных. Для большинства материалов зависимость коэффициента теплопроводности от температуры приближенно можно выразить в виде линейной функции

(9.9)

где λ₀ — значение коэффициента теплопроводности при температуре t₀=0 ⁰С; b — постоянная, определяемая опытным путем.

Наихудшими проводниками теплоты являются газы. Коэффициент теплопроводности газов возрастает с увеличением температуры и составляет 0,006÷0,6 Вт/(м·К). Следует отметить, что верхнее значение относится к гелию и водороду, коэффициент теплопроводности которых в 5—10 раз больше, чем у других газов. Коэффициент теплопроводности воздуха при 0 ⁰С равен 0,0244 Вт/(м·К).

Для жидкости λ=0,07÷0,7 Вт/(м·К) и, как правило, уменьшается с увеличением температуры. Коэффициент теплопроводности воды с увеличением температуры возрастает до максимального значения 0,7 Вт/(м·К) при t=120 ⁰С и дальше уменьшается.

Наилучшими проводниками теплоты являются металлы, у которых λ=20÷418 Вт/(м·К). Самый теплопроводный металл — серебро. Для большинства металлов коэффициент теплопроводности убывает с возрастанием температуры, а также при наличии разного рода примесей. Поэтому коэффициент теплопроводности легированных сталей значительно ниже, чем чистого железа.

Материалы с λ<0,25 Вт/(м·К), обычно применяемые для тепловой изоляции, называют теплоизоляционными. Большинство теплоизоляционных и строительных неметаллических материалов имеют пористое строение, что не позволяет рассматривать их как сплошную среду.

9.4.Дифференциальное уравнение теплопроводности в плоской стенке при граничных условиях первого рода

9.4.1.Дифференциальное уравнение теплопроводности

Решение задач теплопроводности связано с определением поля температур и тепловых потоков. Для установления зависимости между величинами, характеризующими явление теплопроводности, воспользуемся методом математической физики, который рассматривает протекание физических процессов в произвольно выделенном из всего рассматриваемого пространства элементарном объеме и в течение бесконечно малого промежутка времени. Это позволяет пренебречь изменением некоторых величин и существенно упростить выкладки.

При выводе дифференциального уравнения теплопроводности считаем, что тело однородно и изотропно (то есть физические свойства тела не зависят от выбранного в нём направления), физические параметры λ, с(теплоемкость), и ρ (плотность) постоянны, внутренние источники теплоты равномерно распределены в теле. Под внутренними источниками теплоты понимаются тепловыделения, например, в тепловыделяющих элементах атомных реакторов, или при прохождении тока в электрических проводниках. Внутренние источники теплоты характеризуются величиной q_v — количеством теплоты, которое выделяется в единице объема в единицу времени.

В основу вывода положен закон сохранения энергии, согласно которому вся теплота, выделенная внутренними источниками dQ_вн и внесенная извне в элементарный объем путем теплопроводности dQ_m за время dτ, идет на изменение внутренней энергии вещества, содержащегося в этом объеме:

(9.10)

Выделим в теле элементарный параллелепипед с ребрами dx, dy, dz (рис. 9.1). Количество теплоты, которое проходит путем теплопроводности внутрь выделенного объема в направлении оси ОX через элементарную площадку dy·dz за время dτ:

Рис. 9.1. К выводу дифференциального уравнения теплопроводности

На противоположной грани параллелепипеда температура получит приращение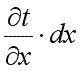

и будет составлять

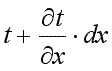Количество тепла, отведенного через эту грань:

Разница количества теплоты, подведенного к элементарному параллелепипеду и отведенного от него, представляет собой теплоту, внесенную путем теплопроводности в направлении оси ОX:

Аналогично:

Полное количество теплоты внесено в элементарный параллелепипед путем теплопроводности

Здесь произведение dx·dy·dz представляет собой объем элементарного параллелепипеда dv. Количество теплоты, которое выделилось в элементарном объеме за счет внутренних источников:

Приращение внутренней энергии можно выразить через массу параллелепипеда ρ·dv, теплоемкость с и приращение температуры :

Подставляя выражения для dQ_m, dQ_вн и dU в уравнение (9.10), после соответствующих сокращений получаем:

(9.11)

Сумма вторых частных производных любой функции в математическом анализе носит название оператора Лапласа и обозначается следующим образом:

Величину называют коэффициентом температуропроводности и обозначают буквой a. В указанных обозначениях уравнение (9.11) примет вид:

(9.12)

Это уравнение называется дифференциальным уравнением теплопроводности или уравнением Фурье и лежит в основе математической теории теплопроводности. Коэффициент температуропроводности a является физическим параметром вещества. Из уравнения (9.12) следует, что изменение температуры во времени для любой точки тела пропорционально величине a.

9.4.2.Краевые условия

Дифференциальное уравнение (9.12) описывает в самом общем виде все без исключения задачи теплопроводности. Для решения конкретной задачи необходимо к дифференциальному уравнению присоединить математическое описание частных ее особенностей. Эти дополнительные данные, которые характеризуют конкретное единичное явление, называются краевыми условиями, или условиями однозначности.

Существуют различные условия однозначности: геометрические — характеризующие форму и размеры тела, в котором протекает процесс теплопроводности; физические — характеризующие физические свойства тела; временные — характеризующие распределение температуры тела в начальный момент времени; граничные — характеризующие взаимодействие тела с окружающей средой. Граничные условия в свою очередь бывают трех родов:

1) первого рода, задается распределение температуры на поверхности тела в функции времени;

2) второго рода, задается плотность теплового потока для всей поверхности тела в функции времени;

3) третьего рода, задаются температура окружающей среды t_ж и закон теплоотдачи между поверхностью тела и окружающей средой — закон Ньютона—Рихмана:

(9.13)

где t_c — температура поверхности тела; α — коэффициент пропорциональности, называемый коэффициентом теплоотдачи, Вт/(м²·К). Коэффициент теплоотдачи численно равен количеству теплоты, отдаваемому или воспринимаемому единицей поверхности в единицу времени при разности температур между поверхностью тела и окружающей средой в один градус. Этот коэффициент учитывает все особенности явлении теплообмена, происходящие между поверхностью тела и окружающей средой. Плотность теплового потока, передаваемого от поверхности тела в окружающую среду,

(9.14)

Согласно закону сохранения энергии, эта теплота равна теплоте, подводимой к поверхности изнутри тела путем теплопроводности:

Переписав последнее уравнение в виде:

(9.15)

получаем математическую формулировку граничных условий третьего рода. В результате решения дифференциального уравнения теплопроводности совместно с условиями однозначности можно найти температурное поле, а на основании закона Фурье — соответствующие тепловые потоки.

9.4.3.Теплопроводность через плоскую стенку при граничных условиях первого рода

Рис. 9.2. Однородная плоская стенка

Рассмотрим однородную плоскую стенку толщиной δ (рис. 9.2). На наружных поверхностях стенки поддерживаются постоянные температуры t_с1 и t_с2. Коэффициент теплопроводности стенки постоянен и равен λ. При стационарном режиме () и отсутствии внутренних источников теплоты (q_v=0) дифференциальное уравнение теплопроводности примет вид:

(9.16)

При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки (ось Оx). В этом случае

и дифференциальное уравнение теплопроводности перепишется в виде:

(9.17)

Граничные условия первого рода запишутся следующим образом: при x=0 t=t_c1; при x=δ t=t_c2. Интегрируя уравнение (9.17), находим

После второго интегрирования получаем

(9.18)

Постоянные С₁ и С₂ определим из граничных условий: при x=0 t=t_c1, С₂=t_c1; при x=δ t=t_c2=С₁·δ+t_c1, отсюда . Подставляя значения С₁ и С₂ в уравнение (9.18), получим уравнение распределения температуры по толщине стенки:

(9.19)

Для определения плотности теплового потока, проходящего через стенку в направлении оси Оx, воспользуемся законом Фурье, согласно которому .

Учитывая, что , получим

(9.20)

Общее количество теплоты, которое передается через поверхность стенки F за время τ,

(9.21)

Отношение называют тепловой проводимостью стенки, обратную ей величину - термическим сопротивлением теплопроводности. Поскольку величина λ зависит от температуры, в уравнения (9.20), (9.21) необходимо подставить коэффициент теплопроводности λ_с, взятый при средней температуре стенки.

Лекции о теплотехнике

Содержание

IS-диаграмма

Водоснабжение, водоподготовка и очистка сточных вод

ЧАСТЬ 2. ТЕПЛОМАССООБМЕН

Тема 9. ТЕПЛОПРОВОДНОСТЬ

9.1.Основные понятия и определения

9.2.Закон Фурье