
Для просмотра сайта используйте Internet Explorer
|
|
Тема 11. ТЕПЛООБМЕН ИЗЛУЧЕНИЕМ
11.1.Основные понятия и определения
Тепловое излучение представляет собой процесс распространения в пространстве внутренней энергии излучающего тела путем электромагнитных волн. Возбудителями этих волн являются материальные частицы, входящие в состав вещества. Для распространения электромагнитных волн не требуется материальной среды, в вакууме они распространяются со скоростью света и характеризуются длиной волны λ или частотой колебаний ν. При температуре до 1500 0С основная часть энергии соответствует инфракрасному и частично световому излучению (λ=0,7÷50 мкм).
Следует отметить, что энергия излучения испускается не непрерывно, а в виде определенных порций — квантов. Носителями этих порций энергии являются элементарные частицы излучения — фотоны, обладающие энергией, количеством движений и электромагнитной массой. При попадании на другие тела энергия излучения частично поглощается ими, частично отражается и частично проходит сквозь тело. Процесс превращения энергии излучения во внутреннюю энергию поглощающего тела называется поглощением. Большинство твердых и жидких тел излучают энергию всех длин волн в интервале от 0 до ∞, то есть имеют сплошной спектр излучения. Газы испускают энергию только в определенных интервалах длин волн (селективный спектр излучения). Твердые тела излучают и поглощают энергию поверхностью, а газы — объемом.
Излучаемая в единицу времени энергия в узком интервале изменения длин волн (от λ до λ+dλ) называется потоком монохроматического излучения Qλ. Поток излучения, соответствующий всему спектру в пределах от 0 до ∞, называется интегральным, или полным, лучистым потоком Q(Вт). Интегральный лучистый поток, излучаемый с единицы поверхности тела по всем направлениям полусферического пространства, называется плотностью интегрального излучения (Вт/м2)
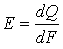 . .
|
(11.1) |
Отсюда
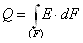 . .
|
Если величина Е одинакова для всех элементов поверхности F, то Q=E·F.
Плотность потока монохроматического излучения носит название спектральной интенсивности излучения Jλ. Она связана с плотностью интегрального излучения уравнением:
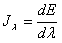
или 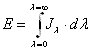 . .
|
(11.2) |
Каждое тело не только излучает, но и поглощает лучистую энергию. Из всего количества падающей на тело лучистой энергии Eпад (Qпад) часть ее Eпог (Qпог) поглощается, часть Еот (Qот) отражается и часть Eпр (Qпр) проходит сквозь тело. Следовательно,
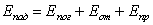 . .
|
(11.3) |
Обозначим
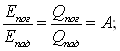
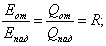
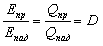 , ,
|
(11.4) |
где А — коэффициент поглощения; R — коэффициент отражения, D — коэффициент пропускания. Тогда А+R+D=1.
Если тело поглощает все падающие на него лучи, то есть A=1, R=О, D=0, оно называется абсолютно черным. Если вся падающая на тело энергия отражается, то R=1, А=О, D=0. Если при этом отражение подчиняется законам геометрической оптики, тело называется зеркальным; при диффузном отражении, когда отраженная лучистая энергия рассеивается по всем направлениям, — абсолютно белым. Если D=1, то A=0 и R=0. Такое тело пропускает все падающие на него лучи и называется абсолютно прозрачным. В природе абсолютно черных, белых и прозрачных тел не существует.
Участвующее в лучистом теплообмене тело, помимо собственного излучения Е, определяемого свойствами излучающего тела и температурой, отражает падающую на него энергию, т. е.
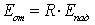 . .
|
(11.5) |
Сумма энергии собственного и отражательного излучения составляет эффективное излучение тела
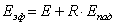 . .
|
(11.6) |
При расчете лучистого теплообмена между телами большое значение имеет результирующее излучение, представляющее собой разность между лучистым потоком, получаемым телом, и лучистым потоком, который оно испускает в окружающее пространство. Для определения плотности потока результирующего излучения qр полагая коэффициент пропускания тела равным нулю составим уравнение баланса энергии, проходящей через плоскости а—а и b—b, одна из которых расположена внутри, а другая снаружи тела вблизи его поверхности (рис. 11.1). Для плоскости а—а
|
|
|
Рис. 11.1. К составлению уравнения баланса энергии.
|
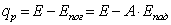 ; ;
|
(11.7) |
для плоскости b—b
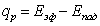 . .
|
(11.8) |
Заметим, что величина qр может быть положительной, отрицательной и равной нулю. Определим зависимость между результирующим и эффективным излучением. Из (11.8)
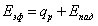 , ,
|
(11.9) |
из (11.7)
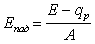 . .
|
(11.10) |
Подставив выражение для Eпад в уравнение (11.9), получаем
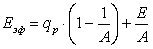 . .
|
(11.11) |
Это уравнение широко используется при расчете лучистого теплообмена между телами.
11.2.Законы теплового излучения
Закон Планка устанавливает зависимость спектральной интенсивности излучения абсолютно черного тела Joλ от длины волны и температуры:
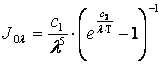 , ,
|
(11.12) |
где λ — длина волны излучения, м; Т — температура излучающего тела, К; c1=3,74·10-16 Вт·м2; c2=1,44·10-2 м·К; e – основание натуральных логарифмов.
Анализ выражения (11.12) показывает, что при λ=0 и λ=∞ Joλ=0, а при некотором промежуточном значении - имеет максимум. Для всех длин волн интенсивность излучения тем выше, чем выше температура. Максимумы кривых с повышением температуры смещаются в сторону более коротких волн.
Закон Стефана — Больцмана. Плотность потока собственного интегрального излучения абсолютно черного тела можно найти на основании закона Планка как суммарную энергию излучения тела по всем длинам волн
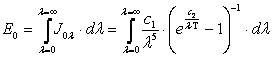 . .
|
(11.13) |
В результате интегрирования найдём
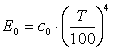 , ,
|
(11.14) |
где с0=5,67 Вт/(м2·К4) — коэффициент излучения абсолютно черного тела. Индекс «О» указывает на то, что рассматривается излучение абсолютно черного тела. Этот закон опытным путем найден Стефаном и теоретически обоснован Больцманом задолго установления закона Планка.
Спектры излучения реальных тел отличны от спектра излучения абсолютно черного тела. При этом спектральная интенсивность излучения тела на любой длине волны никогда не превышает соответствующую спектральную интенсивность излучения абсолютно черного тела. В случае селективного спектра излучения на некоторых участках длин волн интенсивность излучения равна нулю. Частным случаем реальных тел являются серые тела, спектр излучения которых подобен спектру излучения абсолютно черного тела. Интенсивность излучения для каждой длины волны серого тела Jλ составляет одну и ту же долю интенсивности излучения черного тела J0λ, то есть
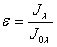 . .
|
(11.15) |
Здесь величина ε — степень черноты тела, зависящая от физических свойств тела, но всегда ε<1. Большинство реальных тел с определенной степенью точности можно считать серыми. Закон Стефана — Больцмана для серого тела с учетом выражения (11.15) имеет вид:
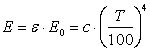 , ,
|
(11.16) |
где с — коэффициент излучения серого тела.
Закон Кирхгофа. Рассмотрим две параллельные поверхности, одна из которых абсолютно черная с температурой Т0, вторая серая с температурой Т и поглощающей способностью A. Расстояние между поверхностями настолько близко, что испускаемые каждой поверхностью лучи обязательно попадают на противоположную. Серая стенка излучает энергию Е и поглощает часть излучаемой черным телом энергии А·E0. Излучаемая серым телом энергия Е и отраженная им энергия (1—А)·E0 попадают на черное тело и поглощаются им.
Результирующее излучение серого тела qр=Е—А·E0. При Т0=Т, qр=0, отсюда
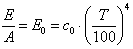 . .
|
(11.17) |
Итак, отношение излучающей способности серого тела к его поглощающей способности при температурном равновесии не зависит от природы тела и равно энергии излучения абсолютно черного тела при той же температуре. Этот закон справедлив и для монохроматического излучения:
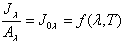 . .
|
(11.18) |
Здесь Аλ — поглощающая способность в узком интервале длин волн. Следовательно, тело, излучающее энергию при какой-либо длине волны, способно поглощать ее при этой же длине волны. На основании равенства (11.17) можно записать Е=А·E0. Однако по (11.16) Е=ε·E0. Таким образом, из закона Кирхгофа также следует, что поглощающая способность серого тела численно равна степени его черноты, то есть А=ε.
Закон Ламберта. Определяет изменение энергии излучения по отдельным направлениям. Согласно этому закону, поток излучения абсолютно черного тела в данном направлении, характеризуемый величиной Jφ, пропорционален потоку излучения в направлении нормали к поверхности Jн и косинусу угла между ними, то есть
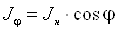 . .
|
(11.19) |
11.3.Теплообмен излучением между телами, разделёнными прозрачной средой
На основании закона лучистого теплообмена можно вывести расчетные уравнения для лучистого теплообмена между твердыми телами. Рассмотрим теплообмен излучением между двумя параллельными пластинами (серыми телами) неограниченных размеров, разделенными прозрачной средой. Для каждой поверхности заданы постоянные во времени температуры Т1 и Т2 (Т1>Т2), поглощающие способности тел А1 и А2. Выведем формулу для определения количества теплоты q12, передаваемой от первой пластины ко второй. Падающий на первую пластину лучистый поток равен эффективному излучению второй пластины Еэф2. Тогда плотность потока результирующего излучения
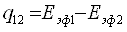 . .
|
(11.20) |
В свою очередь
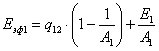 ; ;
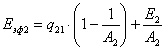 . .
|
При установившемся режиме результирующие потоки для первой и второй пластин одинаковы по величине и противоположны по знаку, т. е. q12=—q21. Подставив значения эффективных излучений в уравнение (11.22), получаем
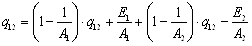 . .
|
Отсюда
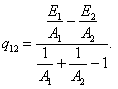
|
Согласно законам Кирхгофа и Стефана—Больцмана,
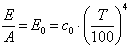 . .
|
Окончательно
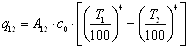 , ,
|
(11.21) |
где
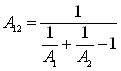
|
называют приведенной поглощающей способностью системы.
11.4.Излучение газов
Одно- и двухатомные газы практически прозрачны для теплового излучения. Значительной излучающей и поглощающей способностью, имеющей практическое значение, обладают трех- и многоатомные газы. Для теплотехнических расчетов наибольший интерес представляют углекислый газ и водяной пар, образующийся при горении топлива. В отличие от твердых тел, имеющих в большинстве сплошные спектры излучения, газы излучают энергию лишь в определенных интервалах длин волн Δλ, называемых полосами спектра. Для лучей других длин волн вне этих полос газы прозрачны, и их энергия излучения равна нулю. Таким образом, излучение и поглощение газов имеют избирательный характер. Если поглощение и излучение энергии в твердых телах происходят в тонком поверхностном слое, то газы излучают и поглощают энергию во всем объеме. Количество поглощаемой газом энергии зависит от числа находящихся в данном объеме микрочастиц газа. Последнее пропорционально толщине газового слоя, характеризуемой длиной пути луча l, парциальному давлению газа р и его температуре Т. Следовательно,
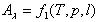 . .
|
(11.22) |
Тогда в соответствии с законом Кирхгофа
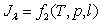 . .
|
(11.23) |
Для каждой полосы спектра
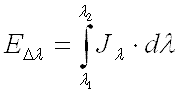 . .
|
Плотность интегрального излучения газовой среды определится суммой их значений для отдельных полос, то есть
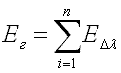 . .
|
Плотность интегрального излучения для двуокиси углерода и водяного пара по опытным данным:
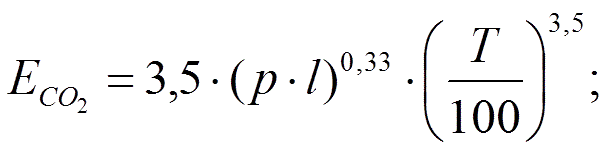
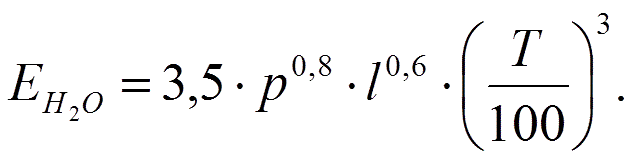
|
Отсюда следует, что законы излучения газов значительно отклоняются от закона Стефана — Больцмана. Однако в основу практических расчетов излучения газов положен именно этот закон. В итоге плотность интегрального излучения с поверхности газового слоя определяется уравнением
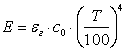 , ,
|
(11.24) |
где εг — степень черноты газового слоя, зависящая от температуры, давления и толщины слоя газа. Для Н2О и СО2 значения εг приводятся в виде номограмм, удобных для практических расчетов. Степень черноты газовых смесей определится как сумма степеней черноты отдельных компонентов. Плотность лучистого потока, передаваемого от газа к окружающим его стенкам (оболочке), вычисляется по уравнению
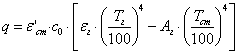 , ,
|
(11.25) |
где εг — степень черноты газа при температуре газа Тг; Аг — поглощающая способность газа при температуре оболочки Тст; 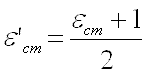 — эффективная степень черноты оболочки.
— эффективная степень черноты оболочки.
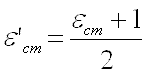 — эффективная степень черноты оболочки.
— эффективная степень черноты оболочки.